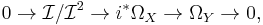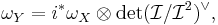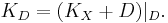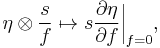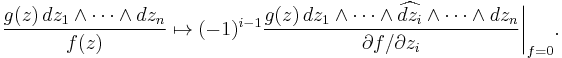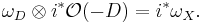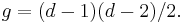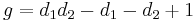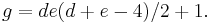Adjunction formula (algebraic geometry)

In mathematics, especially in algebraic geometry and the theory of complex manifolds, the adjunction formula relates the canonical bundle of a variety and a hypersurface inside that variety. It is often used to deduce facts about varieties embedded in well-behaved spaces such as projective space or to prove theorems by induction.

1 Adjunction for smooth varieties
- 1.1 Formula for a smooth subvariety
- 1.2 The particular case of a smooth divisor
2 Poincaré residue
3 Inversion of adjunction
4 Applications to curves
5 See Also
6 References

Adjunction for smooth varieties

Formula for a smooth subvariety

Let X be a smooth algebraic variety or smooth complex manifold and Y be a smooth subvariety of X. Denote the inclusion map Y → X by i and the ideal sheaf of Y in X by 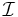$\mathcal{I}$ . The conormal exact sequence for i is

$0 \to \mathcal{I}/\mathcal{I}^2 \to i^*\Omega_X \to \Omega_Y \to 0,$

where Ω denotes a cotangent bundle. The determinant of this exact sequence is a natural isomorphism

$\omega_Y = i^*\omega_X \otimes \operatorname{det}(\mathcal{I}/\mathcal{I}^2)^\vee,$

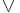where $\vee$ denotes the dual of a line bundle.

The particular case of a smooth divisor

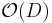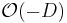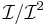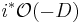Suppose that D is a smooth divisor on X. Its normal bundle extends to a line bundle $\mathcal{O}(D)$ on X, and the ideal sheaf of D corresponds to its dual $\mathcal{O}(-D)$ . The conormal bundle $\mathcal{I}/\mathcal{I}^2$ is $i^*\mathcal{O}(-D)$ , which, combined with the formula above, gives

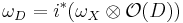$\omega_D = i^*(\omega_X \otimes \mathcal{O}(D))$ .

In terms of canonical classes, this says that

$K_D = (K_X %2B D)|_D.$

Both of these two formulas are called the adjunction formula.

Poincaré residue

The restriction map 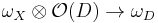$\omega_X \otimes \mathcal{O}(D) \to \omega_D$ is called the Poincaré residue. Suppose that X is a complex manifold. Then on sections, the Poincaré residue can be expressed as follows. Fix an open set U on which D is given by the vanishing of a function f. Any section over U of 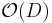$\mathcal{O}(D)$ can be written as s/f, where s is a holomorphic function on U. Let η be a section over U of ω_X. The Poincaré residue is the map

$\eta \otimes \frac{s}{f} \mapsto s\frac{\partial\eta}{\partial f}\bigg|_{f = 0},$

that is, it is formed by applying the vector field ∂/∂f to the volume form η, then multiplying by the holomorphic function s. If U admits local coordinates z₁, ..., z_n such that for some i, ∂f/∂z_i ≠ 0, then this can also be expressed as

$\frac{g(z)\,dz_1 \wedge \dotsb \wedge dz_n}{f(z)} \mapsto (-1)^{i-1}\frac{g(z)\,dz_1 \wedge \dotsb \wedge \widehat{dz_i} \wedge \dotsb \wedge dz_n}{\partial f/\partial z_i}\bigg|_{f = 0}.$

Another way of viewing Poincaré residue first reinterprets the adjunction formula as an isomorphism

$\omega_D \otimes i^*\mathcal{O}(-D) = i^*\omega_X.$

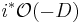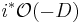On an open set U as before, a section of $i^*\mathcal{O}(-D)$ is the product of a holomorphic function s with the form df/f. The Poincaré residue is the map that takes the wedge product of a section of ω_D and a section of $i^*\mathcal{O}(-D)$ .

Inversion of adjunction

The adjunction formula is false when the conormal exact sequence is not a short exact sequence. However, it is possible to use this failure to relate the singularities of X with the singularities of D. Theorems of this type are called inversion of adjunction. They are an important tool in modern birational geometry.

Applications to curves

The genus-degree formula for plane curves can be deduced from the adjunction formula^[1]. Let C ⊂ P² be a smooth plane curve of degree d and genus g. Let H be the class of a hypersurface in P², that is, the class of a line. The canonical class of P² is −3H. Consequently, the adjunction formula says that the restriction of (d − 3)H to C equals the canonical class of C. This restriction is the same as the intersection product (d − 3)H · dH restricted to C, and so the degree of the canonical class of C is d(d − 3). By the Riemann–Roch theorem, g − 1 = (d − 3)d − g + 1, which implies the formula

$g = (d - 1)(d - 2)/2.$
Similarly^[2], if C is a smooth curve on the quadric surface P¹×P¹ with bidegree (d₁,d₂) (meaning d₁,d₂ are its intersection degrees with a fiber of each projection to P¹), since the canonical class of P¹×P¹ has bidegree (−2,−2), the adjunction formula shows that the canonical class of C is the intersection product of divisors of bidegrees (d₁,d₂) and (d₁−2,d₂−2). The intersection form on P¹×P¹ is 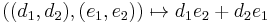$((d_1,d_2),(e_1,e_2))\mapsto d_1 e_2 %2B d_2 e_1$ by definition of the bidegree and by bilinearity, so applying Riemman–Roch gives 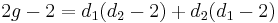$2g-2 = d_1(d_2-2) %2B d_2(d_1-2)$ or

$g = d_1 d_2 - d_1 - d_2 %2B 1$
The genus of a curve C which is the complete intersection of two surfaces D and E in P³ can also be computed using the adjunction formula. Suppose that d and e are the degrees of D and E, respectively. Applying the adjunction formula to D shows that its canonical divisor is (d − 4)H, which is the intersection product of (d − 4)H and D. Doing this again with E, which is possible because C is a complete intersection, shows that the canonical divisor C is the product (d + e − 4)H · dH · eH, that is, it has degree de(d + e − 4). By the Riemann–Roch theorem, this implies that the genus of C is

$g = de(d %2B e - 4) / 2 %2B 1.$

References

^ Hartshorne, chapter V, example 1.5.1
^ Hartshorne, chapter V, example 1.5.2

Phillip Griffiths; Joe Harris (1994). Principles of Algebraic Geometry. Wiley-Interscience. ISBN 0-471-05059-8.
Intersection theory 2nd edition, William Fulton, Springer, ISBN 0-387-98549-2, Example 3.2.12.
Principles of algebraic geometry, Griffiths and Harris, Wiley classics library, ISBN 0-471-05059-8 pp 146–147.
Algebraic geometry, Robin Hartshorne, Springer GTM 52, ISBN 0-387-90244-9, Proposition II.8.20.

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality testing Elliptic curve primality proving

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem for algebraic curves Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves